雑考400 第154号 地平線まで 2000.1.30
────────────────────────────────────────
平地の真ん中に自分の足で立ったとする。周りは見渡す限り地平線である。さて、地平線
までの距離はどのくらいあるだろうか?地表に凹凸がないものとして計算してみる。
地球の半径=r、地平線までの距離=χ、地平線の地点=P、地球の中心=O、
地表から高さhメートルの目の位置=Qとする。
地平線の1地点Pに地球への接線を引けば、三角形OPQは、Pを直角、OQを斜辺と
する直角三角形となる。
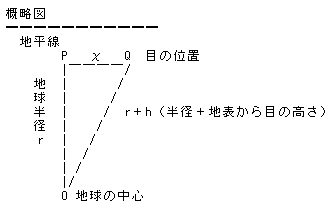
ここで、
OP=r(地球半径)
PQ=χ(地平線までの距離)
OQ=r(地球半径)+h(高さ)
であるから、
ピタゴラスの定理により、
r^2+χ^2=(r+h)^2 ; ^2は二乗を表す
となる。これを変形して、
χ^2=(r+h)^2−r^2
答えは正の平方根であるから、
![]()
となる。広辞苑によれば、地球の極半径=6,357km なので、これを基に計算すると、
h=1.5m(目の高さ) → χ(地平線までの距離)≒4.4km
h=2m(背の高い人) → χ≒5.0km
h=10m(普通のビルの3〜4階?) → χ≒11.3km
h=243m(東京都庁の天辺) → χ≒55.6km
h=333m(東京タワーの天辺) → χ≒65.1km
h=3,776m(富士山の頂上) → χ≒219.1km
h=8,848m(チョモランマの頂上) → χ≒335.5km
h=11.9km(高度39000フィートのジェット旅客機) → χ≒389.2km
となる。あくまで理論値であるが、見渡す限り地平線の平地に自分の足で立ったとして、
その地平線までは、歩いて1時間程度である。地平線も案外近い。一方、高層ビル等から
はかなり遠くまで見える。当たり前ではあるが、火の見櫓や見張り台が高いわけだ。
※今回は400字をオーバーしましたが、了承願います。
────────────────────────────────────────
mail:NBA00155@nifty.ne.jp http://www.geocities.co.jp/HeartLand-Keyaki/1755
__________________________________
( 「雑考400」は、40字×10行の、1分で読める系統立っていない考察や考証です )
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄